1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
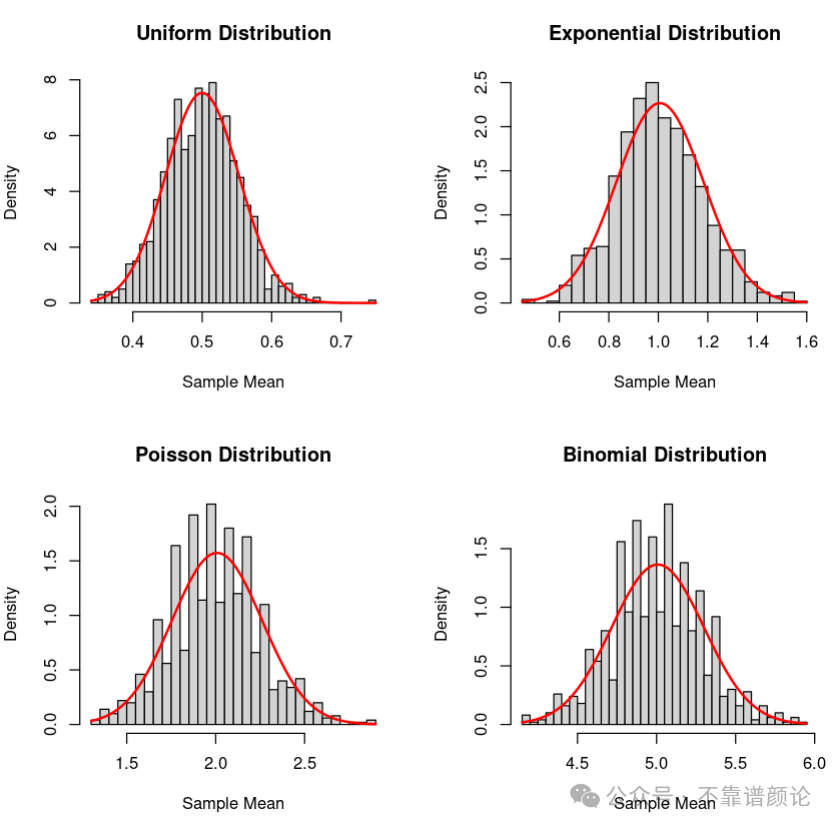
# Demonstration of the Central Limit Theorem (CLT)
# Set common parameters
n <- 1000 # Number of samples
sample_size <- 30 # Size of each sample
# Prepare a 2x2 plot layout
par(mfrow=c(2,2))
# 1. Uniform Distribution
sample_means_uniform <- replicate(n, mean(runif(sample_size, min=0, max=1)))
hist(sample_means_uniform, breaks=40, probability=TRUE, main="Uniform Distribution", xlab="Sample Mean")
curve(dnorm(x, mean=mean(sample_means_uniform), sd=sd(sample_means_uniform)), add=TRUE, col="red", lwd=2)
# 2. Exponential Distribution
sample_means_exponential <- replicate(n, mean(rexp(sample_size, rate=1)))
hist(sample_means_exponential, breaks=40, probability=TRUE, main="Exponential Distribution", xlab="Sample Mean")
curve(dnorm(x, mean=mean(sample_means_exponential), sd=sd(sample_means_exponential)), add=TRUE, col="red", lwd=2)
# 3. Poisson Distribution
sample_means_poisson <- replicate(n, mean(rpois(sample_size, lambda=2)))
hist(sample_means_poisson, breaks=40, probability=TRUE, main="Poisson Distribution", xlab="Sample Mean")
curve(dnorm(x, mean=mean(sample_means_poisson), sd=sd(sample_means_poisson)), add=TRUE, col="red", lwd=2)
# 4. Binomial Distribution
sample_means_binomial <- replicate(n, mean(rbinom(sample_size, size=10, prob=0.5)))
hist(sample_means_binomial, breaks=40, probability=TRUE, main="Binomial Distribution", xlab="Sample Mean")
curve(dnorm(x, mean=mean(sample_means_binomial), sd=sd(sample_means_binomial)), add=TRUE, col="red", lwd=2)
# Reset plot layout
par(mfrow=c(1,1))
|